1.小明用一张长32厘米,宽20厘米的长方形纸,最多能剪( )个半径是2厘米的圆形纸片。
A.50 B.40 C.160
【分析】这张长32厘米,宽20厘米的长方形纸,长能剪32÷(2×2)=8(张)半径是2厘米的圆形纸片,宽能剪20÷(2×2)=5(张),这张纸最多能剪成8×5=40(张)这样的圆形纸片。
【解答】32÷(2×2)=8(张) 20÷(2×2)=5(张) 8×5=40(张);
答:最多能剪成半径是7厘米的圆形纸版40个,故选:B.
【点评】注意:不能用长方形纸版的面积除以每张圆形纸版的面积,因为圆不能密铺.
2.小明的妈妈要买一块台布盖住家中一张直径1米的圆形桌面,你认为选( )种比较合适。
A.120厘米×120厘米 B.120厘米×80厘米
C.3140平方厘米 D.314平方厘米
【分析】因为是一张直径1米的圆形桌面,所以需用的台布的边长应大于1米,对照给出的答案进行比较,得出A适合;进而选择即可。
【解答】因为120×120的桌布的边长为120厘米,大于圆桌的直径100厘米,所以选用120×120的桌布比较合适,故选:A。
【点评】解答此题的关键:应明确所需的桌布的边长应大于或等于圆桌的直径。
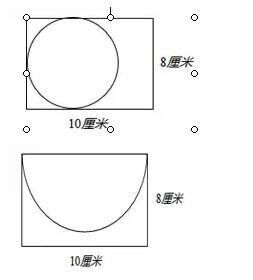
3.在一个长是10厘米,宽是8厘米的长方形中画一个最大的圆,这个圆的周长是( )厘米;如果画一个最大的半圆,这个半圆的周长是( )厘米。
【分析】由题意画出下图:根据圆的周长公式C=πd求出圆的周长;根据半圆的周长=πd÷2+d,代入数据解答即可。
【解答】(1)3.14×8=25.12(厘米);
(2)3.14×10÷2+10=15.7+10=25.7(厘米)
答:在一个长是10厘米,宽是8厘米的圆中画一个最大的圆,这个圆的周长是25.12厘米;如果画一个最大的半圆,这个半圆的周长是25.7厘米。故答案为:25.12,25.7。
【点评】此题考查了圆和半圆的周长的计算方法,此题关键是根据长方形内最大圆和半圆的特点,先确定出这个圆和半圆的直径。
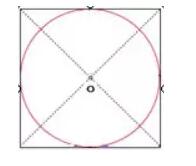
4.在边长4厘米的正方形中画一个最大的圆。(在图上要画出你是怎样找到圆心的)
【分析】正方形的两条对角线的交点为圆心,以正方形的边长4厘米为直径画圆。
【解答】如图:
【点评】本题主要考查了正方形及正方形里面的最大的圆的作法。
5.一个圆形纸板的半径为r,如果将这个纸板沿一条直径剪开,得到两个半圆,每个半圆的周长大约是( )。
A.3.14r B.5.14r C.6.28r
【分析】要求半圆的周长,根据半圆的周长=圆的周长÷2+直径,计算即可得到正确答案。
【解答】 3.14×2×r÷2+2r=3.14r+2r =5.14r
答:每个半圆的周长是5.14r,故选:B。
【点评】解答此题的关键是:特别注意半圆的周长要加上直径。
6.在右图中A、B是圆的直径AB的两个端点,图中阴影部分的周长( )空白部分的周长。
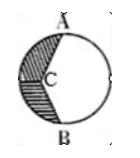
A.小于 B.大于 C.等于
【分析】根据周长的含义,可知阴影部分的周长=线段AC+线段BC+半圆弧长,空白部分的周长=线段AC+线段BC+半圆弧长;进而得出结论。
【解答】由分析知:阴影部分的周长=线段AC+线段BC+半圆弧长,空白部分的周长=线段AC+线段BC+半圆弧的长;所以阴影部分的周长=空白部分的周长,故选:C。
【点评】解答此题应根据题意,进行求出阴影部分和空白部分的周长,然后比较即可。
7.钟面的时针长8厘米,一昼夜时针尖端走( )厘米。
【分析】时针长8厘米,即时针所画的圆的半径为8厘米,一昼夜是24小时,即时针一昼夜走2圈,因此,根据圆的周长公式,求出一圈的周长,再乘2即可。
【解答】C=2πr=2π×8=16π(厘米),所以尖端一共走了:16π×2=32π(厘米)
答:一昼夜这根时针的尖端走了32π厘米,故答案为:32π。
【点评】解答此题的关键是,知道时针的针尖一昼夜走的路程,就是以半径为8厘米圆的周长的2倍,由此列式解答即可。
8.半径为2厘米的圆,它的周长和面积相比( )。
A.相等 B.面积大 C.周长大 D.不能比较
【分析】圆的周长是指围成圆一周的长度,面积则是指圆的大小,周长用长度单位,面积用面积单位,它们不能比较大小。
【解答】因为周长和面积的概念不同,单位名称不同,所以周长和面积不能比较大小,故选:D。
【点评】此题主要考查周长和面积的意义。
9.一个圆环,它的外圆直径是内圆直径的两倍,则这个圆环的面积( )。
A.比内圆面积大 B.比内圆面积小
C.与内圆面积一样大 D.无法判断
【分析】根据“外圆直径是内圆直径的2倍”,知道外圆半径是内圆半径的2倍,由此根据圆的面积公式S=πr2,分别用内圆的半径表示出两个圆的面积,进而得出圆环的面积,再与内圆的面积比较,从而做出选择。
【解答】设内圆的半径为r,则外圆的半径为2r,
所以圆环的面积是π(2r)2-πr2=3πr2>πr2,
所以这个圆环的面积比内圆面积大;故选:A。
【点评】本题主要考查了利用圆的面积公式S=πr2计算圆环的面积。
10.把一个圆的半径扩大3倍,圆的周长就扩大( )倍,面积扩大( )倍。
A.3 B.6 C.9
【分析】根据圆的周长和面积公式可知:圆的半径扩大n倍,圆的周长就扩大n倍,面积扩大n2倍。
【解答】由圆的周长和面积公式可知:一个圆的半径扩大3倍,圆的周长就扩大3倍,面积扩大3×3=9倍。
如:圆的半径为1,周长为2π,面积π;
圆的半径扩大3倍为3,周长为6π,面积9π;
周长扩大6π÷2π=3倍,面积扩大9π÷π=9倍,故选:A,C。
【点评】考查了圆的周长和面积,关键是理解和掌握圆的周长和面积与圆的半径之间的关系。
11.如图,正方形的面积是16平方厘米,则圆的面积是( )平方厘米。
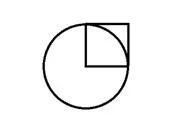
A.50.24 B.25.12 C.12.56
【分析】分析条件“小正方形面积是16平方厘米”并结合图可以看出,这个小正方形的边长也就是这个圆的半径,这个小正方形的面积也就是圆半径的平方,根据圆的面积S=πr2,就可以算出答案。
【解答】S=πr2=3.14×16=50.24(平方厘米)
答:圆的面积是50.24平方厘米,故选:A。
【点评】这道题直接利用半径的平方,而不是圆面积公式中的半径,这一点不要因为做题习惯而忽略。
12.在一个半径是4米的圆形花坛四周铺一条1米宽的砖路,砖路的面积是( )平方米。

【分析】如图所示,求砖路的面积,实际上就是求圆环的面积,即大圆的面积减小圆的面积就是圆环的面积,大圆的半径为(4+1)米,小圆的半径为4米,代入圆的面积公式即可求出砖路的面积。
【解答】3.14×(4+1)2-3.14×42
=3.14×(25-16)
=3.14×9
=28.26(平方米)
答:砖路的面积是28.26平方米,故答案为:28.26。
【点评】解答此题的关键是明白:砖路的面积就是圆环的面积,用大圆的面积减小圆的面积即可。